打码

使用js实现简单的框选

2019/06/02 js

使用 js 来实现一个简单的功能，长按 350ms 可选中，选中后不松开鼠标可以进行框选。主要的难点是几个鼠标的事件，以及框选范围的判断。

盒子集合.png

假设有如上的集合需要框选。

框选效果.png

长按 350 ms

在鼠标按下之后，发起个定时器，350ms 之后如果鼠标还未抬起，就判断为长按。同时如果在 350ms 内鼠标移出了盒子，或者抬起鼠标，便清除定时器。

// 开始按下
startTouch = e => {
  const handle = function() {
    if (!globalTouch) {
      clearTimeout(touchTimer)
      touchTimer = null
    }
    e.target.removeEventListener(isMobile ? 'touchmove' : 'mouseout', handle)
  }
  e.target.addEventListener(isMobile ? 'touchmove' : 'mouseout', handle)
  touchTimer = setTimeout(() => {
    addClass(e.target, 'active')
    globalTouch = true
  }, 350)
}
// 鼠标抬起
endTouch = e => {
  if (touchTimer) {
    clearTimeout(touchTimer)
    touchTimer = null
  }
  globalTouch = false
  startPoint = { x: null, y: null }
}

框选判断

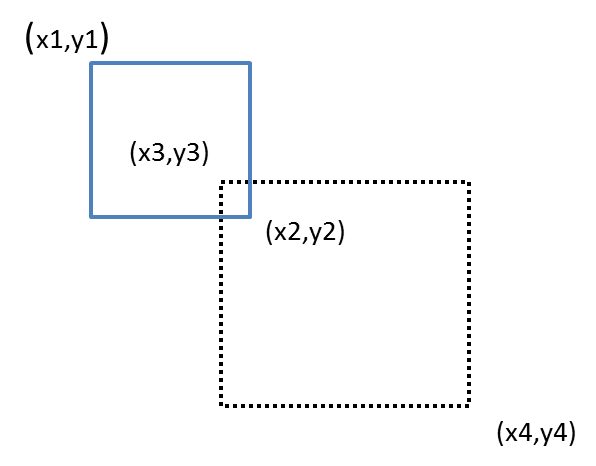
图片1.png

每一个盒子的范围判断如上图所示，一个矩形只需要确定左上和右下的坐标就可以判断范围了。如果需要判断是否在框选范围内，判断起来可能有点复杂。但是反过来，判断两个矩形不相交就简单了，只要判断 x1 在 x4 的右边(x1 > x4 )，y1 在 y4 的下面(y1 > y4)，x2 在 x3 的左边(x2 < x3)，y2 在 y3 的上面 (y2 < y3)，只要满足上面的一种情况，这两个矩形就永远不会相交。

核心代码

function isInArea(elm, start, end) {
  const startPoint = {
    x: Math.min(start.x, end.x),
    y: Math.min(start.y, end.y),
  }
  const endPoint = {
    x: Math.max(start.x, end.x),
    y: Math.max(start.y, end.y),
  }
  const xStart = elm.offsetLeft
  const xEnd = elm.offsetLeft + elm.clientWidth
  const yStart = elm.offsetTop
  const yEnd = elm.offsetTop + elm.clientHeight
  if (
    xStart >= endPoint.x || // x1 > x4
    yStart >= endPoint.y || // y1 > y4
    xEnd <= startPoint.x || // x2 < x3
    yEnd <= startPoint.y // y2 < y3
  ) {
    removeClass(elm, 'active') // 不在框选范围内
  } else {
    addClass(elm, 'active') // 在范围内，高亮
  }
}
// 当鼠标开始移动后便调用上面的函数判断。
overTouch = e => {
  if (globalTouch) {
    ;[].slice
      .call(document.querySelectorAll('.box'))
      .map(function(element, index) {
        isInArea(element, startPoint, {
          x: !isMobile ? e.pageX : e.targetTouches[0].pageX,
          y: !isMobile ? e.pageY : e.targetTouches[0].pageY,
        })
      })
  }
}

最后

整体效果在 codepen 上，感兴趣的小伙伴可以点击看看。 CodePen 地址

Search

    Table of Contents